6÷2(1+2)
I wrote a (very long) blog post about those viral math problems and am looking for feedback, especially from people who are not convinced that the problem is ambiguous.
It's about a 30min read so thank you in advance if you really take the time to read it, but I think it's worth it if you joined such discussions in the past, but I'm probably biased because I wrote it :)
You're viewing a single thread.
Having read your article, I contend it should be:
P(arentheses)
E(xponents)
M(ultiplication)D(ivision)
A(ddition)S(ubtraction)
and strong juxtaposition should be thrown out the window.
Why? Well, to be clear, I would prefer one of them die so we can get past this argument that pops up every few years so weak or strong doesn't matter much to me, and I think weak juxtaposition is more easily taught and more easily supported by PEMDAS. I'm not saying it receives direct support, but rather the lack of instruction has us fall back on what we know as an overarching rule (multiplication and division are equal). Strong juxtaposition has an additional ruling to PEMDAS that specifies this specific case, whereas weak juxtaposition doesn't need an additional ruling (and I would argue anyone who says otherwise isn't logically extrapolating from the PEMDAS ruleset). I don't think the sides are as equal as people pose.
To note, yes, PEMDAS is a teaching tool and yes there are obviously other ways of thinking of math. But do those matter? The mathematical system we currently use will work for any usecase it does currently regardless of the juxtaposition we pick, brackets/parentheses (as well as better ordering of operations when writing them down) can pick up any slack. Weak juxtaposition provides better benefits because it has less rules (and is thusly simpler).
But again, I really don't care. Just let one die. Kill it, if you have to.
It's like using literally to add emphasis to something that you are saying figuratively. It's not objectively "wrong" to do it, but the practice is adding uncertainty where there didn't need to be any, and thus slightly diminishes our ability to communicate clearly.
I think anything after (whichever grade your country introduces fractions in) should exclusively use fractions or multiplication with fractions to express division in order to disambiguate. A division symbol should never be used after fractions are introduced.
This way, it doesn't really matter which juxtaposition you prefer, because it will never be ambiguous.
Anything before (whichever grade introduces fractions) should simply overuse brackets.
This comment was written in a couple of seconds, so if I missed something obvious, feel free to obliterate me.
A division symbol should never be used after fractions are introduced.
But a fraction is a single term, 2 numbers separated by a division is 2 terms. Terms are separated by operators and joined by grouping symbols.
I think weak juxtaposition is more easily taught
Except it breaks the rules which already are taught.
the PEMDAS ruleset
But they're not rules - it's a mnemonic to help you remember the actual order of operations rules.
Just let one die. Kill it, if you have to
Juxtaposition - in either case - isn't a rule to begin with (the 2 appropriate rules here are The Distributive Law and Terms), yet it refuses to die because of incorrect posts like this one (which fails to quote any Maths textbooks at all, which is because it's not in any textbooks, which is because it's wrong).
Except it breaks the rules which already are taught.
It isn't, because the 'currently taught rules' are on a case-by-case basis and each teacher defines this area themselves. Strong juxtaposition isn't already taught, and neither is weak juxtaposition. That's the whole point of the argument.
But they’re not rules - it’s a mnemonic to help you remember the actual order of operations rules.
See this part of my comment: "To note, yes, PEMDAS is a teaching tool and yes there are obviously other ways of thinking of math. But do those matter? The mathematical system we currently use will work for any usecase it does currently regardless of the juxtaposition we pick, brackets/parentheses (as well as better ordering of operations when writing them down) can pick up any slack. Weak juxtaposition provides better benefits because it has less rules (and is thusly simpler)."
Juxtaposition - in either case - isn’t a rule to begin with (the 2 appropriate rules here are The Distributive Law and Terms), yet it refuses to die because of incorrect posts like this one (which fails to quote any Maths textbooks at all, which is because it’s not in any textbooks, which is because it’s wrong).
You're claiming the post is wrong and saying it doesn't have any textbook citation (which is erroneous in and of itself because textbooks are not the only valid source) but you yourself don't put down a citation for your own claim so... citation needed.
In addition, this issue isn't a mathematical one, but a grammatical one. It's about how we write math, not how math is (and thus the rules you're referring to such as the Distributive Law don't apply, as they are mathematical rules and remain constant regardless of how we write math).
It isn’t, because the ‘currently taught rules’ are on a case-by-case basis and each teacher defines this area themselves
Nope. Teachers can decide how they teach. They cannot decide what they teach. The have to teach whatever is in the curriculum for their region.
Strong juxtaposition isn’t already taught, and neither is weak juxtaposition
That's because neither of those is a rule of Maths. The Distributive Law and Terms are, and they are already taught (they are both forms of what you call "strong juxtaposition", but note that they are 2 different rules, so you can't cover them both with a single rule like "strong juxtaposition". That's where the people who say "implicit multiplication" are going astray - trying to cover 2 rules with one).
See this part of my comment... Weak juxtaposition provides better benefits because it has less rules (and is thusly simpler)
Yep, saw it, and weak juxtaposition would break the existing rules of Maths, such as The Distributive Law and Terms. (Re)learn the existing rules, that is the point of the argument.
citation needed
Well that part's easy - I guess you missed the other links I posted. Order of operations thread index Text book references, proofs, the works.
this issue isn’t a mathematical one, but a grammatical one
Maths isn't a language. It's a group of notation and rules. It has syntax, not grammar. The equation in question has used all the correct notation, and so when solving it you have to follow all the relevant rules.
Nope. Teachers can decide how they teach. They cannot decide what they teach. The have to teach whatever is in the curriculum for their region.
Yes, teachers have certain things they need to teach. That doesn't prohibit them from teaching additional material.
That’s because neither of those is a rule of Maths. The Distributive Law and Terms are, and they are already taught (they are both forms of what you call “strong juxtaposition”, but note that they are 2 different rules, so you can’t cover them both with a single rule like “strong juxtaposition”. That’s where the people who say “implicit multiplication” are going astray - trying to cover 2 rules with one).
Yep, saw it, and weak juxtaposition would break the existing rules of Maths, such as The Distributive Law and Terms. (Re)learn the existing rules, that is the point of the argument.
Well that part’s easy - I guess you missed the other links I posted. Order of operations thread index Text book references, proofs, the works.
You argue about sources and then cite yourself as a source with a single reference that isn't you buried in the thread on the Distributive Law? That single reference doesn't even really touch the topic. Your only evidence in the entire thread relevant to the discussion is self-sourced. Citation still needed.
Maths isn’t a language. It’s a group of notation and rules. It has syntax, not grammar. The equation in question has used all the correct notation, and so when solving it you have to follow all the relevant rules.
You can argue semantics all you like. I would put forth that since you want sources so much, according to Merriam-Webster, grammar's definitions include "the principles or rules of an art, science, or technique", of which I think the syntax of mathematics qualifies, as it is a set of rules and mathematics is a science.
That doesn’t prohibit them from teaching additional material
Correct, but it can't be something which would contradict what they do have to teach, which is what "weak juxtaposition" would do.
a single reference
I see you didn't read the whole thread then. Keep going if you want more. Literally every Year 7-8 Maths textbook says the same thing. I've quoted multiple textbooks (and haven't even covered all the ones I own).
mathematics is a science
Actually you'll find that assertion is hotly debated.
Correct, but it can’t be something which would contradict what they do have to teach, which is what “weak juxtaposition” would do.
Citation needed.
I see you didn’t read the whole thread then. Keep going if you want more. Literally every Year 7-8 Maths textbook says the same thing. I’ve quoted multiple textbooks (and haven’t even covered all the ones I own).
If I have to search your 'source' for the actual source you're trying to reference, it's a very poor source. This is the thread I searched. Your comments only reference 'math textbooks', not anything specific, outside of this link which you reference twice in separate comments but again, it's not evidence for your side, or against it, or even relevant. It gets real close to almost talking about what we want, but it never gets there.
But fine, you reference 'multiple textbooks' so after a bit of searching I find the only other reference you've made. In the very same comment you yourself state "he says that Stokes PROPOSED that /b+c be interpreted as /(b+c). He says nothing further about it, however it's certainly not the way we interpret it now", which is kind of what we want. We're talking about x/y(b+c) and whether that should be x/(yb+yc) or x/y * 1/(b+c). However, there's just one little issue. Your last part of that statement is entirely self-supported, meaning you have an uncited refutation of the side you're arguing against, which funnily enough you did cite.
Now, maybe that latter textbook citation I found has some supporting evidence for yourself somewhere, but an additional point is that when providing evidence and a source to support your argument you should probably make it easy to find the evidence you speak of. I'm certainly not going to spend a great amount of effort trying to disprove myself over an anonymous internet argument, and I believe I've already done my due diligence.
Citation needed.
So you think it's ok to teach contradictory stuff to them in Maths? 🤣 Ok sure, fine, go ahead and find me a Maths textbook which has "weak juxtaposition" in it. I'll wait.
Your comments only reference ‘math textbooks’, not anything specific
So you're telling me you can't see the Maths textbook screenshots/photo's?
outside of this link which you reference twice in separate comments but again, it’s not evidence for your side, or against it, or even relevant
Lennes was complaining that literally no textbooks he mentioned were following "weak juxtaposition", and you think that's not relevant to establishing that no textbooks used "weak juxtaposition" 100 years ago?
We’re talking about x/y(b+c) and whether that should be x/(yb+yc) or x/y * 1/(b+c).
It's in literally the first textbook screenshot, which if I'm understanding you right you can't see? (see screenshot of the screenshot above)
you have an uncited refutation of the side you’re arguing against, which funnily enough you did cite.
Ah, no. Lennes was complaining about textbooks who were obeying Terms/The Distributive Law. His own letter shows us that they all (the ones he mentioned) were doing the same thing then that we do now. Plus my first (and later) screenshot(s).
Also it's in Cajori, but I didn't find it until later. I don't remember what page it was, but it's in Cajori and you have the reference for it there already.
you should probably make it easy to find the evidence you speak of
Well I'm not sure how you didn't see all the screenshots. They're hard to miss on my computer!
So you think it’s ok to teach contradictory stuff to them in Maths? 🤣 Ok sure, fine, go ahead and find me a Maths textbook which has “weak juxtaposition” in it. I’ll wait.
You haven't provided a textbook that has strong juxtaposition.
So you’re telling me you can’t see the Maths textbook screenshots/photo’s?
That's not a source, that's a screenshot. You can't look up the screenshot, you can't identify authors, you can't check for bias. At best I can search the title of the file you're in that you also happened to screenshot and hope that I find the right text. The fact that you think this is somehow sufficient makes me question your claims of an academic background, but that's neither here nor there. What does matter is that I shouldn't have to go treasure hunting for your sources.
And, to blatantly examine the photo, this specific text appears to be signifying brackets as their own syntactic item with differing rules. However, I want to note that the whole issue is that people don't agree so you will find cases on both sides, textbook or no.
Lennes was complaining that literally no textbooks he mentioned were following “weak juxtaposition”, and you think that’s not relevant to establishing that no textbooks used “weak juxtaposition” 100 years ago?
You are welcome to cite the specific wording he uses to state this. As far as I can tell, at least in the excerpt linked, there is no such complaint.
You haven’t provided a textbook that has strong juxtaposition
I told you, in my thread - multiple ones. You haven't provided any textbooks at all that have "weak juxtaposition". i.e. you keep asking me for more evidence whilst never producing any of your own.
At best I can search the title of the file you’re in that you also happened to screenshot and hope that I find the right text
I didn't "just happen" to include the name of the textbook and page number - that was quite deliberate. Not sure why you don't want to believe a screenshot, especially since you can't quote any that have "weak juxtaposition" in the first place.
BTW I just tried Googling it and it was the first hit. You're welcome.
What does matter is that I shouldn’t have to go treasure hunting for your sources.
You don't - the screenshots of the relevant pages are right there. You're the one choosing not to believe what is there in black and white, in multiple textbooks.
with differing rules
Yeah, I wrote about inconsistency in textbooks here (also includes another textbook saying you have to expand brackets first), but also elsewhere in the thread is an example where they have been consistent throughout. Regardless of when they remove brackets, in every single case they multiply the coefficient over what's inside the brackets as the first step (as per BEDMAS, and as per the screenshot in question which literally says you must do it before you remove brackets).
people don’t agree
People who aren't high school Maths teachers (the ones who actually teach this topic). Did you notice that neither The Distributive Law nor Terms are mentioned at any point whatsoever? That's like saying "I don't remember what I did at Xmas, so therefore it's ambiguous whether Xmas ever happened at all, and anyone who says it definitely did is wrong".
no such complaint.
So what do you think he is complaining about?
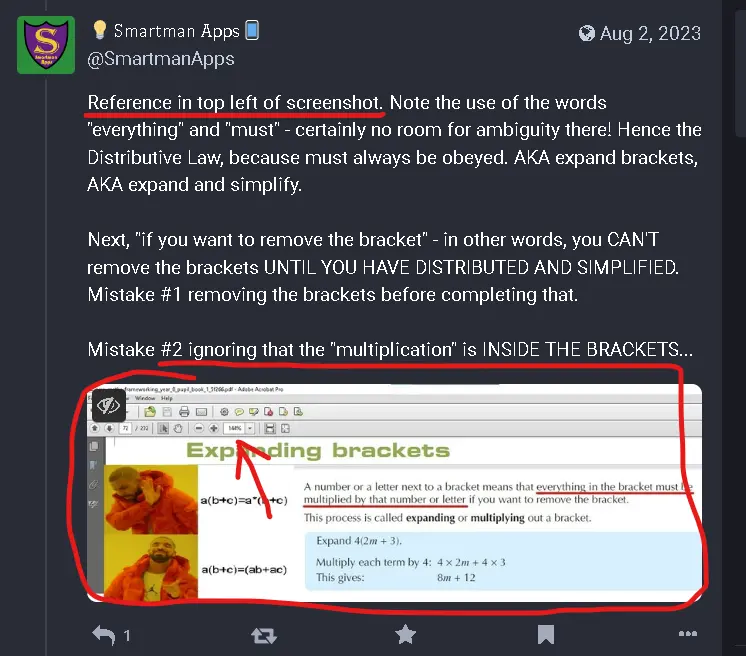
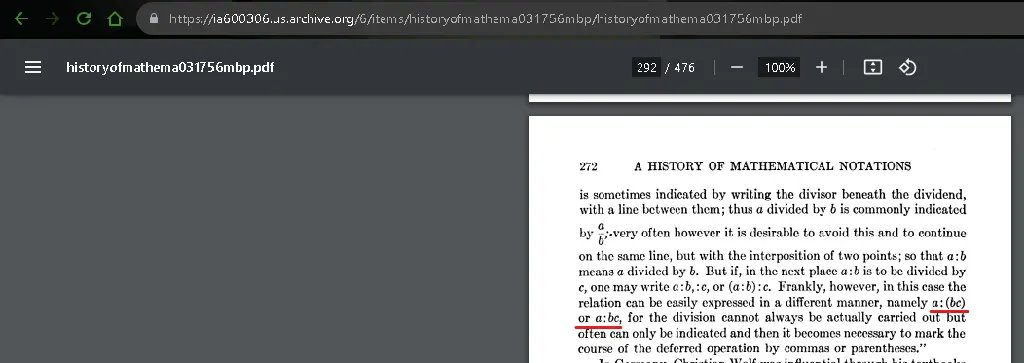
I told you, in my thread - multiple ones. You haven’t provided any textbooks at all that have “weak juxtaposition”. i.e. you keep asking me for more evidence whilst never producing any of your own.
You seem to have missed the point. I'm holding you to your own standard, as you are the one that used evidence as an excuse for dismissal first without providing evidence for your own position.
I didn’t “just happen” to include the name of the textbook and page number - that was quite deliberate. Not sure why you don’t want to believe a screenshot, especially since you can’t quote any that have “weak juxtaposition” in the first place. BTW I just tried Googling it and it was the first hit. You’re welcome.
You seem to have missed the point. You're providing a bad source and expecting the person you're arguing against to do legwork. I never said I couldn't find the source. I'm saying I shouldn't have to go looking.
You don’t - the screenshots of the relevant pages are right there. You’re the one choosing not to believe what is there in black and white, in multiple textbooks.
You've provided a single textbook, first of all. Second of all, the argument is that both sides are valid and accepted depending on who you ask, even amongst educated echelons. The fact there exists textbooks that support strong juxtaposition does nothing to that argument.
But you want some evidence, so here's an article from someone who writes textbooks speaking on the ambiguity. Again, the ambiguity exists and your claim that it doesn't according to educated professors is unsubstantiated. There are of course professors who support strong juxtaposition, but there are also professors who support weak juxtaposition and professors that merely acknowledge the ambiguity exist. The rules of mathematics you claim are set in stone aren't relevant (and aren't as set in stone as you imagine) but that's not entirely relevant. What is relevant is there is an argument and it's not just uneducated folk mistaking the 'truth'.
People who aren’t high school Maths teachers (the ones who actually teach this topic). Did you notice that neither The Distributive Law nor Terms are mentioned at any point whatsoever? That’s like saying “I don’t remember what I did at Xmas, so therefore it’s ambiguous whether Xmas ever happened at all, and anyone who says it definitely did is wrong”.
You are correct, I suppose a mathematics professor from Harvard (see my previous link for the relevant discussion of the ambiguity) isn't at the high school level.
But wait, there's more. Here's another source from another mathematics professor. This one 'supports' weak juxtaposition but really mostly just points at the ambiguity. Which again, is what I'm going for, that the ambiguity exists and one side is not immediately justified/'correct'.
So what do you think he is complaining about?
That's a leading question and is completely unhelpful to the discussion. I asked you to point out where exactly, and with what wording, your position is supported in the provided text. Please do that.
Here you go - I found I did save a screenshot of Cajori saying ab and (ab) are the same thing - I didn't think I had.
P.S. if you DID want to indicate "weak juxtaposition", then you just put a multiplication symbol, and then yes it would be done as "M" in BEDMAS, because it's no longer the coefficient of a bracketed term (to be solved as part of "B"), but a separate term.
6/2(1+2)=6/(2+4)=6/6=1
6/2x(1+2)=6/2x3=3x3=9
Division comes before Multiplication, doesn't it? I know BODMAS.
That makes no sense. Division is just multiplication by an inverse. There's no reason for one to come before another.
This actually explains alot. Murica is Pemdas but Canadian used Bodmas so multiply is first in America.
As far as I understand it, they're given equal weight in the order of operations, it's just whichever you hit first left to right.
Ah, but if you use the rules BODMSA (or PEDMSA) then you can follow the letter order strictly, ignoring the equal precedence left-to-right rule, and you still get the correct answer. Therefore clearly we should start teaching BODMSA in primary schools. Or perhaps BFEDMSA. (Brackets, named Functions, Exponentiation, Division, Multiplication, Subtraction, Addition). I'm sure that would remove all confusion and stop all arguments. ... Or perhaps we need another letter to clarify whether implicit multiplication with a coefficient and no symbol is different to explicit multiplication... BFEIDMSA or BFEDIMSA. Shall we vote on it?
Don't need any extra letters - just need people to remember the rules around expanding brackets in the first place.
Obviously more letters would make the mnemonic worse, not better. I was making a joke.
As for the brackets 'the rules around expanding brackets' are only meaningful in the assumed context of our order of operations. For example, if we instead all agreed that addition should be before multiplication, then a×(b+c) would "expand" to a×b+c, because the addition is before multiplication anyway and the brackets do nothing.
I was making a joke.
Fair enough, but my point still stands.
if we instead all agreed that addition should be before multiplication
...then you would STILL have to do multiplication first. You can't change Maths by simply agreeing to change it - that's like saying if we all agree that the Earth is flat then the Earth is flat. Similarly we can't agree that 1+1=3 now. Maths is used to model the real world - you can't "agree" to change physics. You can't add 1 thing to 1 other thing and have 3 things now, no matter how much you might want to "agree" that there is 3, there's only 2 things. Multiplying is a binary operation, and addition is unary, and you have to do binary operators before unary operators - that is a fact that no amount of "agreeing" can change. 2x3 is actually a contracted form of 2+2+2, which is why it has to be done before addition - you're in fact exposing the hidden additions before you do the additions.
the brackets do nothing
The brackets, by definition, say what to do first. Regardless of any other order of operations rules, you always do brackets first - that is in fact their sole job. They indicate any exceptions to the rules that would apply otherwise. They perform no other function. If you're going to no longer do brackets first then you would simply not use them at all anymore. And in fact we don't - when there are redundant brackets, like in (2)(1+2), we simply leave them out, leaving 2(1+2).
I believe you're conflating the rules of maths with the notation we use to represent mathematical concepts. We can choose whatever notation we like to mean anything we like. There is absolutely nothing stopping us from choosing to interpret a+b×c as (a+b)×c rather than a+(b×c). We don't even have to write it like that at all. We could write a,b,c×+. (And sometimes people do write it like that.) Notation is just a way to communicate. It represents the maths, but it is not itself the maths. Some notation is more convenient or more intuitive than others. × before + is a very convenient choice, because it easier to express mathematical truths clearly and concisely - but nevertheless, it is still just a choice.
I believe you’re conflating the rules of maths with the notation we use to represent mathematical concepts.
You think a Maths teacher doesn't know the difference?
There is absolutely nothing stopping us from choosing to interpret a+b×c as (a+b)×c
Yes there is - the underlying Maths. 2x3 is short for 2+2+2, which is therefore why you have to expand multiplications before doing additions. If you "chose" to interpret 2+3x4 (which we KNOW is equal to 14, because 3x4=3+3+3+3 by definition) as (2+3)x4, you would get 20, which is clearly wrong, since 20 isn't equal to 14.
We don’t even have to write it like that at all
No that's right, because it IS written differently in different languages, but regardless of how you write it, it doesn't change that 2+3x4=14 - the underlying Maths doesn't change regardless of how you decide to write it. Maths is literally universal.
× before + is a very convenient choice
It's not a choice, it's a consequence of the fact that x is shorthand for +. i.e. 2x3=2+2+2.
it is still just a choice
It is a consequence of the definitions of what each operator does. If x is a contraction of +, then we have to expand x before we do +. If it were the other way around then we'd have to do it the other way around. Anything which is a contraction of something else has to be expanded first.
Yeah 100% was not taught that. Follow the pemdas or fail the test. Division is after Multiply in pemdas.
I put the equation into excel and get 9 which only makes sense in bodmas.
It doesn't make sense in BODMAS either. Expanding Brackets has precedence of... Brackets, not "multiplication" - "Multiplication" refers literally to multiplication signs, of which there are none in this question.
The y(n+1) is same as yn + y if you removed the "6÷" part. It's implied multiplication.
The y(n+1) is same as yn + y
No, it's the same as (yn+y). You can't remove brackets unless there is only 1 term left inside.
if you removed the “6÷” part. It’s
...The Distributive Law.
Well I'm not seeing the difference here. Yn+y= yn+y = y(n+1) = y × (n +1) I think we agree with that.
Ok, that's a start. In your simple example they are all equal, but they aren't all the same.
yn+y - 2 terms
y(n+1) - 1 term
y×(n +1) - 2 terms
To see the difference, now precede it with a division, like in the original question...
1÷yn+y=(1/yn)+y
1÷y(n+1)=1/(yn+y)
1÷y×(n +1)=(n +1)/y
Note that in the last one, compared to the second one, the (n+1) is now in the numerator instead of in the denominator. Welcome to why having the (2+2) in the numerator gives the wrong answer.